最高のコレクション (a+b)^3/2 expansion 262164-(a+b)^3/2 expansion

For Raspberry pi B / 3 / 2 Model B/ 4 Model B T GPIO For Raspberry Pi B 3 2 Breakout Expansion Board Kit 40Pin Cabl DIY E7I7 $252 Free shipping T GPIO For Raspberry Pi B 3 2 Breakout Expansion Board 40Pin Cabl Kit Hot P5V4 $279 Free shippingQuestion is ⇒ Curve A in Fig 11 compared to curves B and C shows the following type of expansion, Options are ⇒ (A) pV"=C, (B) isothermal, (C) adiabatic, (D) free expansion, (E) throttling, Leave your comments or Download question paperTo find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize our results as follows The Binomial Theorem Using Pascal's Triangle

Solved Problem Sheet 9 11 10 1 3 2 9 2 1 1 5 A Giv Chegg Com

(a+b)^3/2 expansion

(a+b)^3/2 expansion-The final answer (ab)^5=a^55a^4b10a^3b^210a^2b^35a^1b^4b^5 The binomial theorem tells us that if we have a binomial (ab) raised to the n^(th) power the result will be (ab)^n=sum_(k=0)^nc_k^n *a^(nk)*b^(n) where " "c _k^n= (n!)/(k!(nk)!) and is read "n CHOOSE k equals n factorial divided by k factorial (nk) factorial" So (ab)^5=a^55a^4b10a^3b^210a^2b^35a^1b^4A^3 3a^2b 3ab^2 b^3 Use the Binomial expansion (note the exponents sum to the power in each term) (xy)^3 = _3C_0x^3y^0 _3C_1x^2y^1 _3C_2x^1y^2 _3C_3x^0y^3

What Is The Formula Of Math A B 3 Math Quora

Click here👆to get an answer to your question ️ The number of terms in the expansion of (a 4b)^3(a 4b)^3 ^2 areB −, where A and B are constants, (a) find the values of A and B (3) (b) Hence, or otherwise, find the series expansion of f(x), in ascending powers of x, up to and including the term in x3, simplifying each term (6) June 06 8 f(x) = 2 2 (1 3 )(2 ) 3 16 x x x − = (2 x) B (2 x)2 C , x < 3 1 (a) Find the values of A and C(x1)^2 7x (x3)^2 = 33 (x 5)(x 5) expand the brackets (x1)(x1) 7x (x3)(x3) = 33 (x5)(x5) multiply the brackets together using whichever method (i use the smiley face method) (x^2) 1 2x 7x (x^2) 9 6x = 33 (x^2) 25 collect the like terms either side of the equals sign (2x^2) 15x 10 = 33 (x^2) 25

Finding powers 2 i close to powers b j of other numbers b is comparatively easy, and series representations of ln(b) are found by coupling 2StarTechcom PEXUS12A3 2Port USB PCIe Card with 10Gbps/port USB 31/32 Gen 2 TypeA PCI Express 30 x2 Host Controller Expansion Card AddOn Adapter Card Full/Low Profile Windows & Linux Type PCI Express to USB Card;Ex 81,1 Not in Syllabus CBSE Exams 21 Ex 81,2 Important Not in Syllabus CBSE Exams 21 Ex 81,3 Not in Syllabus CBSE Exams 21 Ex 81,4 Important Not in

What I want to do with this video is cover something called the triple product expansion or Lagrange's formula, sometimes And it's really just a simplification of the cross product of three vectors, so if I take the cross product of a, and then b cross c And what we're going to do is, we can express this really as sum and differences of dotCoefficients So far we have a 3 a 2 b ab 2 b 3 But we really need a 3 3a 2 b 3ab 2 b 3 We are missing the numbers (which are called coefficients) Let's look at all the results we got before, from (ab) 0 up to (ab) 3In a third layer, the logarithms of rational numbers r = a / b are computed with ln(r) = ln(a) − ln(b), and logarithms of roots via ln n √ c = 1 / n ln(c) The logarithm of 2 is useful in the sense that the powers of 2 are rather densely distributed;

Solved Expand The Following Expressions Using The Binomia Chegg Com

Misc 9 Expand Using Binomial Theorem 1 X 2 2 X 4 Miscellaneou

Problem 95 (ECE March 1996) The equation whose roots are the reciprocals of the roots of 2×2 – 3x – 5 = 0 is A 5×2 3x – 2 = 0;All USB 32 Gen 2x2 products use the TypeC connector, but not all USBC ports are USB 32 Gen 2x2 A USBC port can be either Gbps USB 32 Gen 2x2 or 10Gbps USB 32 Gen 2 A USB TypeA port canIf the seventh term from the beginning and end in the binomial expansion of (3 2 3 3 1 ) n are equal, find n View solution If the number of terms in the expansion of ( 1 2 x − 3 x 2 ) n is 36, then n equals

Amazon Com Xygstudy Arpi600 For Raspberry Pi 4 3 2 1 Model B B A Plus Supports Arduino Xbee Module With Various Interface Io Expansion Board Computers Accessories

Binomial Theorem

The power of power rule \eqref{power_power} allows us to define fractional exponents For example, rule \eqref{power_power} tells us that \begin{gather*} 9^{1/2}=(3^2)^{1/2} = 3^{2 \cdot 1/2} = 3^1 = 3 \end{gather*} Taking a number to the power of $\frac{1}{2}$ undoes taking a number to the power of 2 (or squaring it)The ASUS ThunderboltEX 3 Expansion Card provides a single Thunderbolt 3 port for motherboards that have an available PCIe 30 x4 slot, Thunderbolt header, and DisplayPort The Thunderbolt 3 port sports a reversible USB TypeC interface and delivers a maximum throughput of 40 Gb/s The port supports USB 31 at up to 10 Gb/s as well as DisplayPort 12, allowing you to connect multiple displays, of the binomial expansion of (2 kx) 7 where k is a constant Give each term in its simplest form (4) Given that the coefficient of x 2 is 6 times the coefficient of x, (b) find the value of k (2) (Total 6 marks) 4 Find the first 3 terms, in ascending powers of x, of the binomial expansion of ( ) −3 2 x 5, giving each

Solved Find The Sixth Term Of The Binomial Expansion Course Hero

Solved Problem Sheet 9 11 10 1 3 2 9 2 1 1 5 A Giv Chegg Com

Divisibility by 3 Divisibility by 9 formula (a b)2= a2 2ab b2 notes Expansion of (a b)2= a2 2ab b2 In the above figure, the side of the square PQRS is (x y) ∴ A( PQRS) = (x y)2 The square PQRS is divided into 4 rectangles I, II, III, IVFor example, when n = 5, each term in the expansion of (a b) 5 will look like this a 5 − k b k k will successively take on the values 0 through 5 (a b) 5 = a 5 a 4 b a 3 b 2 a 2 b 3 ab 4 b 5 Note Each lower index is the exponent of bWhere b is a positive real number, and the argument x occurs as an exponent For real numbers c and d, a function of the form () = is also an exponential function, since it can be rewritten as = () As functions of a real variable, exponential functions are uniquely characterized by the fact that the growth rate of such a function (that is, its derivative) is directly proportional to the

A B 3 2 Expansion

What Is A B 3 Quora

If the roots of the quadratic equation ax2 bx c = 0 are 3 and 2 and a, b, and c are all whole numbers, find a b c A 12;Free expand & simplify calculator Expand and simplify equations stepbystepWe can choose two a's from 3 factors in C(3,2) ways=3 We can choose a remaining letter in 1 way, so the coefficients of a 2 are 3·1 ways 3a 2 (bc) 3ab 2 3b 2 c Similarly for the b 2 terms 3b 2 (ac) 3ac 2 3bc 2 And the c 2 3c 2 (ab) 6abc The remaining terms are abc's We can choose an a in 3 ways, and then a b in 2 ways, and then we

Msbshse Solutions For Class 8 Maths Part 1 Chapter 5 Expansion Formulae Download For Free

Multinomial Expansion

Find 31 ways to say expansion, along with antonyms, related words, and example sentences at Thesauruscom, the world's most trusted free thesaurus(a b c) 2 = (a b c)(a b c) = a(a b c) b(a b c) c(a b c) = a 2 ab ac ba b 2 bc ca cb c 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2acIf the seventh term from the beginning and end in the binomial expansion of (3 2 3 3 1 ) n are equal, find n View solution If the number of terms in the expansion of ( 1 2 x − 3 x 2 ) n is 36, then n equals

4 The Binomial Theorem

Binomial Theorem

Square Formulas(a b)2= a2 b2 2ab(a − b)2= a2 b2− 2aba2− b2= (a − b) (a b)(x a) (x b) = x2 (a b) x ab(a b c)2= a2 b2 c2 2ab 2bc 2caA1/3 a1/3 a1/3 = a (24) (a1/3)3 = a (25) (a2)1/3 = (a1/3)2 = a2∕3 (26) (a1/3)1/4 = a1/3 1/4 = (a1/4)1/3 (27) (a b)1/3 = a1/3 b1/3 (28) (a / b)1/3 = a1/3 / b1/3 (29) (1 / a)1/3 = 1 / a1/3 = a1/3 (30) Sponsored Links Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and moreOf a positive integer n is defined by n!

General And Middle Term Binomial Theorem Formula Videos Examples

Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9

How to Expand (abc) 2?We can choose two a's from 3 factors in C(3,2) ways=3 We can choose a remaining letter in 1 way, so the coefficients of a 2 are 3·1 ways 3a 2 (bc) 3ab 2 3b 2 c Similarly for the b 2 terms 3b 2 (ac) 3ac 2 3bc 2 And the c 2 3c 2 (ab) 6abc The remaining terms are abc's We can choose an a in 3 ways, and then a b in 2 ways, and then weCheck here stepbystep solution of 'The number of terms in the expansion of {(a4b)^3 (a−4b)^3}^2 is' question at Instasolv!

Expansion Of A Low Ms 7 2 5 2 B Middle Ms 3 2 1 2 And C Download Scientific Diagram

What Is The Formula Of Math A B 3 Math Quora

A 7 b 7 = (a b)(a 6 – a 5 b a 4 b 2 – a 3 b 3 a 2 b 4 – ab 5 b 6) 11 If n is odd, then a n b n = (a b)(a nThis means that the expansion of (ab)6 is (ab)6 = a6 6a5b15a4b2 a3b3 15a2b4 6ab5 b6 2 14 Factorial notation The factorial n!External USB Ports 2 x USB 32 USB TypeA (9 pin, Gen 2, 10 Gbps) Internal Ports 1 x SATA Power (15 pin)

Multinomial Expansion

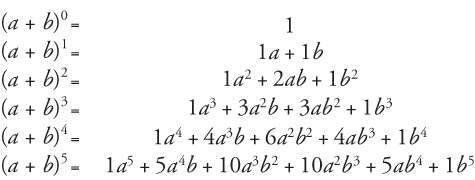
Binomial Coefficients And The Binomial Theorem

The expansion of alcohol in a thermometer is one of many commonly encountered examples of thermal expansion, the change in size or volume of a given mass with temperatureHot air rises because its volume increases, which causes the hot air's density to be smaller than the density of surrounding air, causing a buoyant (upward) force on the hot air4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n come from the nth row of Pascal's= 5×4×3×2×1 = 1 and 8!

What Is A B 3 Quora

The Binomial Theorem Fractional Powers Expanding 1 2x 1 3 Youtube

B 3×2 – 5x – 3 = 0 ;26 If a;band kare positive real numbers, b6=1 ;k6=1,thenlog b a= log k a log k b 27 log b a= 1 log a b where a;bare positive real numbers, a6=1 ;b6=1 28 if a;m;n are positive real numbers, a6= 1 and if log a m=log a n,then m=n Typeset by AMSTEX1) State whether the following rational numbers will have terminating decimalexpansion or a nonterminating repeating expansion of decimal a) 17/8 Solution 17/8 = 17/(2 3 x 5 0) As the denominator is of the form 2 n 5 m so the expansion of decimal of 17/8 is terminating b) 64/255 solution 64/255 = 64/ (5 x 3 x 17) Clearly, 255 is

Expanding Binomials Video Polynomials Khan Academy

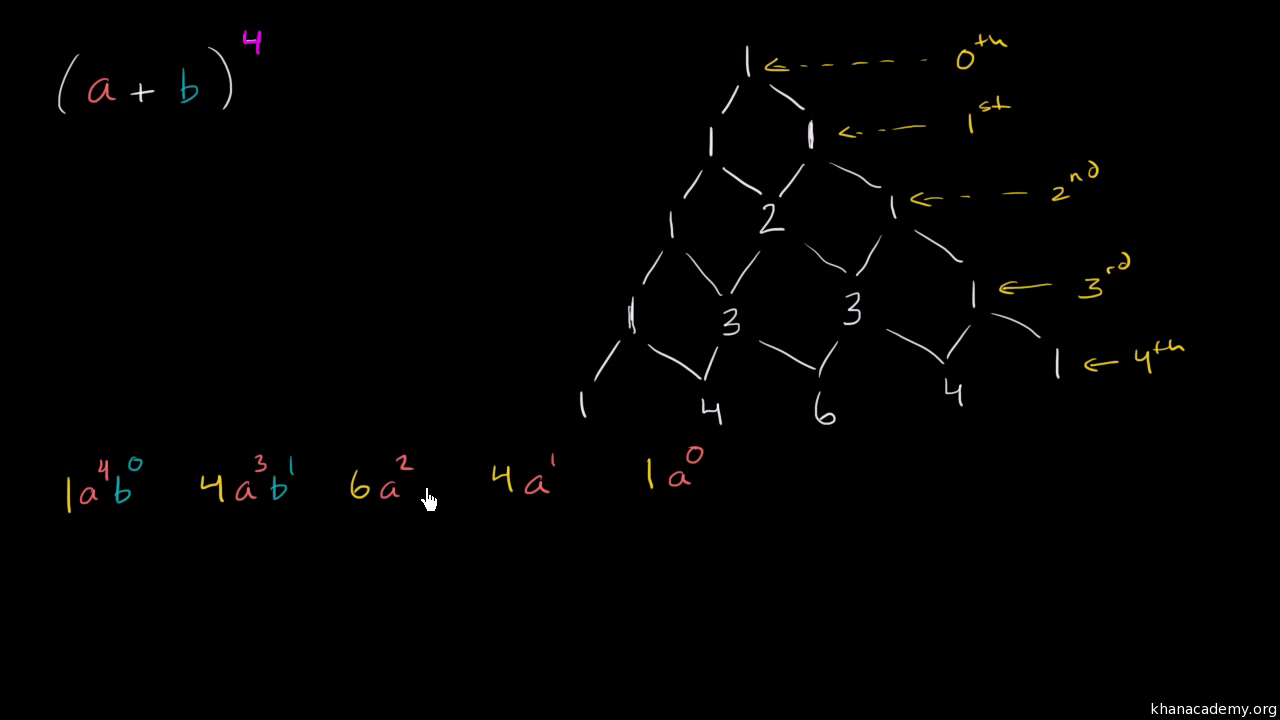
Pascal S Triangle And Binomial Expansion Video Khan Academy

So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) Generally It is, of course, often impractical to write out Pascal"s triangle every time, when all that we need to know are the entries on the nth line Clearly, the first number on the nth line is 1 The= (1000 3) 2 Expanding using formula = 1000 2 3 2 2 × 1000 × 3 By further calculation = 9 6000 = (iii) (102) 2 It can be written as = (10 02) 2 Expanding using formula = 10 2 02 2 2 × 10 × 02 By further calculation = 100 004 4 = 24 Use (a – b) 2 = a 2 – 2ab – b 2 to evaluate the2 ab b2 ) 9a3 b3 = (a b) (a 2 ab b2 ) 10(a b)2 (a b) 2 = 4ab 11(a b)2 (a b) 2 = 2(a 2 b2 ) 12If a b c =0, then a3 b3 c3 = 3 abc INDICES AND SURDS 1 am a n = a m n 2 am m n a an = − 3 (a ) am n mn= 4 (ab) a bm m m= 5 a am m b bm = 6 a 1, a 00 = ≠ 7 m 1 a am − = 8 a a x yx

Solved Use The Cofactor Expansion Theorem To Evaluate The Chegg Com

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

C 5×2 – 2x – 3 = 0 ;GPIO pin corresponding to the reference function GPIO multiplexing multiple interfaces contrast Raspberry Pi For raspberry pi B / 3 / 2 Model B= 8×7×6×5×4×3×2×1 = 403 We work with the convention that 1!

Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf

Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf

= 1 and 0!View Binomial Expansion 1docx from IB MATH Math 1 at Western University Binomial Expansion 1 1 Expand and simplify (a) (p q)3 (b) (x 1)3 (e) 3x – 1)3 (f) (2x 5)3 2 Expand and simplify (a)= n(n−1)(n−2)···(3)(2)(1) so for example 5!

Partial Fraction Expansion Repeated Factors Video Khan Academy

Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf

2B 3B 4 Channel RPi Relay Module Expansion Board for Raspberry Pi 3 2 A B 4 Channel RPi Relay Module Expansion Board for Raspberry Pi 3 2 A B 2B 3B NoteThe Raspberry Pi has 40Pin and 26Pin connectors This product is only compatible with the 40Pin Raspberry Pi Raspberry Pi GPIO interface For connecting Raspberry PiCORBIN The Corbin Arq Plant is continuing to move forward with the announcement of $10 million expansion funding from Community Trust Bank, Inc (CTBI) guaranteed by the USDA's business and= a 32 b 2 = ab 2 a nk b k = a 33 b 3 = b 3 It works like magic!

The Binomial Theorem Example 2 Youtube

Madasmaths Com Archive Maths Booklets Basic Topics Various Binomial Expansions Exam Questions Pdf

Given a2b2c23=2(abc) Expanding RHS we get a2b2c23=2a2b2c Carrying RHS to LHS > a2b2c232a2b2c=0 We have a22a, so we try if any identity can be applied here a22a1 is the expansion for (a1)2 Since we have three variables a,b,cDefinition binomial A binomial is an algebraic expression containing 2 terms For example, (x y) is a binomial We sometimes need to expand binomials as follows (a b) 0 = 1(a b) 1 = a b(a b) 2 = a 2 2ab b 2(a b) 3 = a 3 3a 2 b 3ab 2 b 3(a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4(a b) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5Clearly, doing this byThe Second Period of Expansion Rome's growth threatened another great power, the city of Carthage (KARthidge), in North Africa During the second period of expansion, from 264 to 146 BCE, Rome and Carthage fought three major wars Through these wars, Rome gained control of North Africa, much of Spain, and the island of Sicily

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

Example 1 Expand X 2 3 X 4 Binomial Theorem Class 11

Prentice Hall Mathematics, Algebra 2 (0th Edition) Edit edition Problem 70E from Chapter 68 What is the third term in the expansion of (a − b)7?F −21a5 Get solutionsCity of London Academy 2 4 (a) Find the binomial expansion of in ascending powers of x up to and including the term in x3, simplifying each term (4) (b) Show that, when x = the exact value of √(1 – 8x) is (2) (c) Substitute into the binomial expansion in part (a) and hence obtain an4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n come from the nth row of Pascal's

Compute The Determinant Of The Matrix By Cofactor Expansion 3 2 5 1 1 4 3 Homeworklib

What Is The Binomial Expansion Of Math 1 X 2 Math Quora

The Middle Term In The Expansion Of 2x 3 3 2x 2 2n Is A

If T2 T3 In The Expansion Of A B N And T3 T4 In The A B N 3 Are Equal Then N

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Gpio Multifunction Extended Expansion Board For Raspberry Pi B 3 2 Model B Business Industrial Electronic Components Semiconductors

T Gpio For Raspberry Pi B 3 2 Breakout Expansion Board Diy Kit 40pin Cabl O5y5 Ebay

Coefficients A 1 2 And B 2a 3 2 In The Long Wave Expansion Equation 31 Download Scientific Diagram

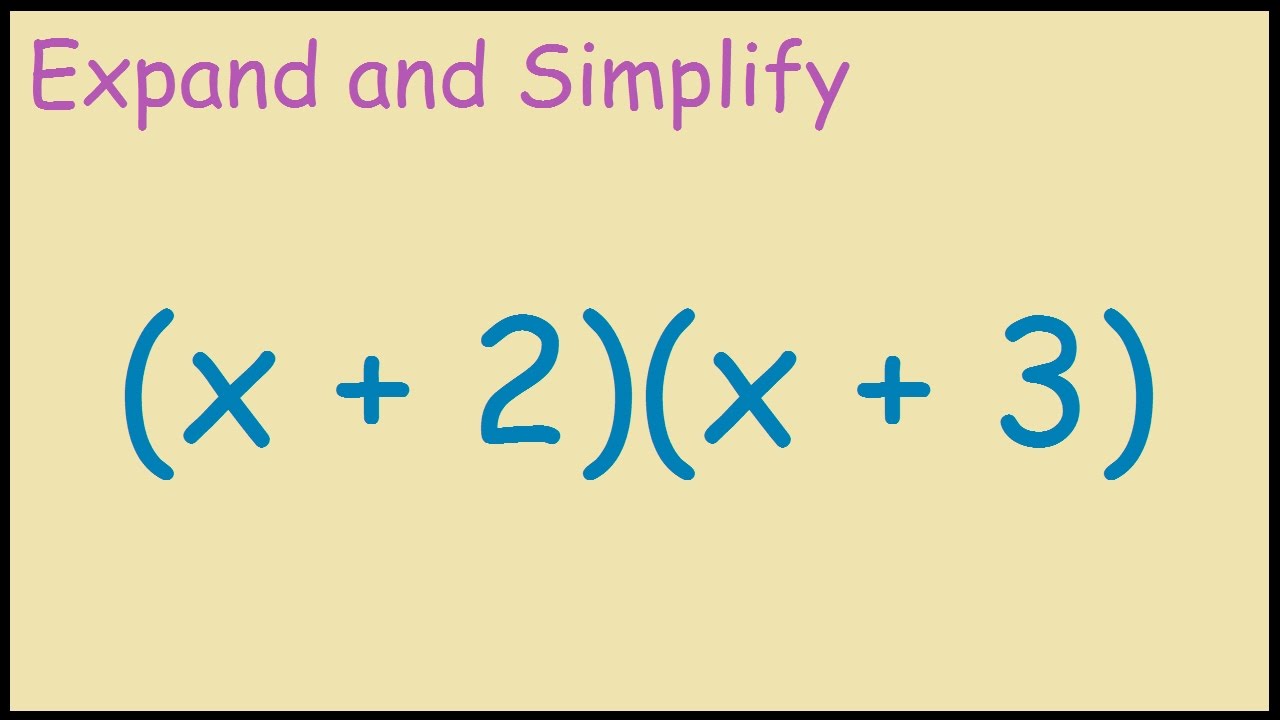
X 2 X 3 Expand And Simplify Youtube

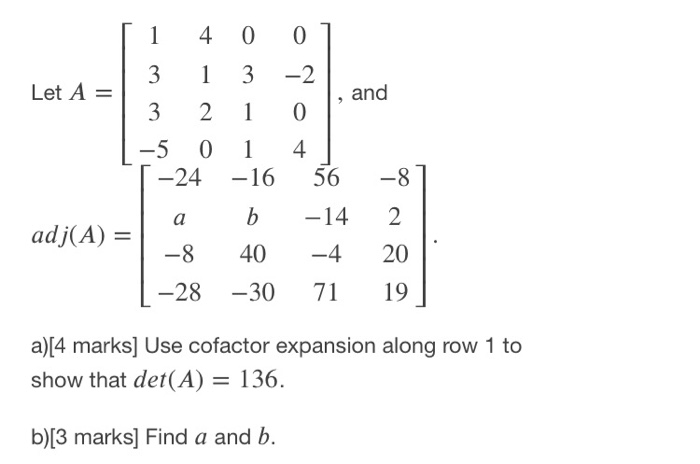
Solved 1 4 0 0 3 1 3 2 Let A And 0 3 2 5 0 24 1 1 1 Chegg Com

Binomial Theorem Binomial Theorem Term 1 Unit 3 Ppt Video Online Download

Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf

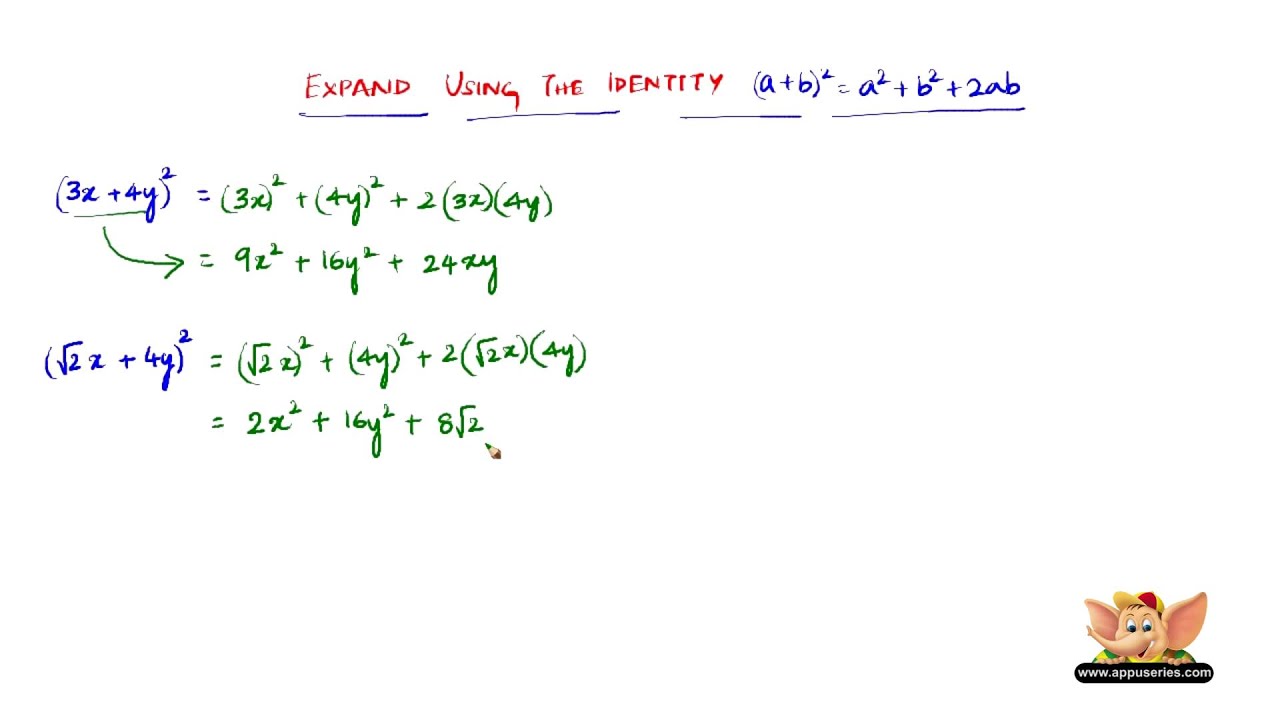
How To Expand Using The Identity A B 2 B2 2ab Youtube

Need Help Asap Which Of The Following Is The Correct Expanded Form For The Series Below A 0 1 Brainly Com

What Is The Expansion Of A B C 3 Quora

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

What Is The Formula Of Math A 3 B 3 Math Quora

2

Amazon Com Makerfocus Raspberry Pi Expansion Board 4 Channel Relay Board Module Power Relay Module For Raspberry Pi 4b 3 Model B Raspberry Pi 3 2 Model B No Programming Required Programmable Computers Accessories

What Is The Formula Of Math A B 3 Math Quora

4 The Sum Of All Rational Terms In The Expansion Of Left 3 17 5 12 Right 14 Is N Begin Array L L L L Text A 3 2 Text B 3 2 5 7 Text C 3 7 5

Search Q A 5e3 B 5e3 Tbm Isch

Solved Show That Det 1 1 1 1 A B C D A 2 B 2 C 2 D 2 A 3 Chegg Com

Solved 1 2 1 And B 0 Compute A B 2 And 2abb2 Are T Chegg Com

What Is A B 3 Quora

What Is The Correct Formula Of Math A B 3 Math Quora

Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download

What Is The Formula Of Math A B 3 Math Quora

Binomial Theorem Examples Solutions Examples Videos Worksheets Activities

Sec 2 Math Algebraic Expansion Gcse Basics Youtube

1 Two Wires A And B Of Same Length Same Area Of Cross Section Having The

Solved In Exercises 17 Use The Column Row Expansion O Chegg Com

3 3 Determinants By Expansion Wolfram Demonstrations Project

Solved Find The Partial Fractions Expansion For The Follo Chegg Com

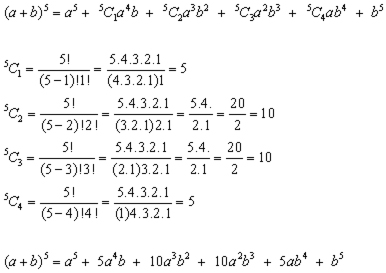
The Binomial Theorem Algebra Pure Mathematics From A Level Maths Tutor

Lesson 2 Power Rules I Will Understand How To Expand And Simplify Basic And Complex Exponents Ppt Download

Solved Find The Coefficient A A In The Expansion Of Chegg Com

Expand I 3 2 4 Maths Questions

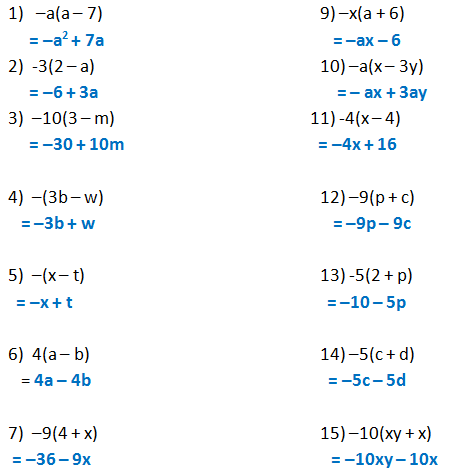
Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths

Amazon Com Quickbuying 1pcs T Type Adapter Expansion Board For Raspberry Pi 3 2 Model B B A Zero For Bread Board Experiment Computers Accessories

Q Tbn And9gcrerbjjqzrmqv Kqpsvyx4wtx7pwzhnyvlfcm0guaa Usqp Cau

A B 3 2 Expansion

11 1 Pascal S Triangle And The Binomial Theorem Ppt Download

What Is The Formula Of Math A 3 B 3 Math Quora

Jee Mains 18 The Expansion Of 3x 2 1 2 Is Valid In Ascending Powers Of X If X Lies I Youtube

Solved 2 Let A And B Be 4x4 Matrices Such That Det A Chegg Com

Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf

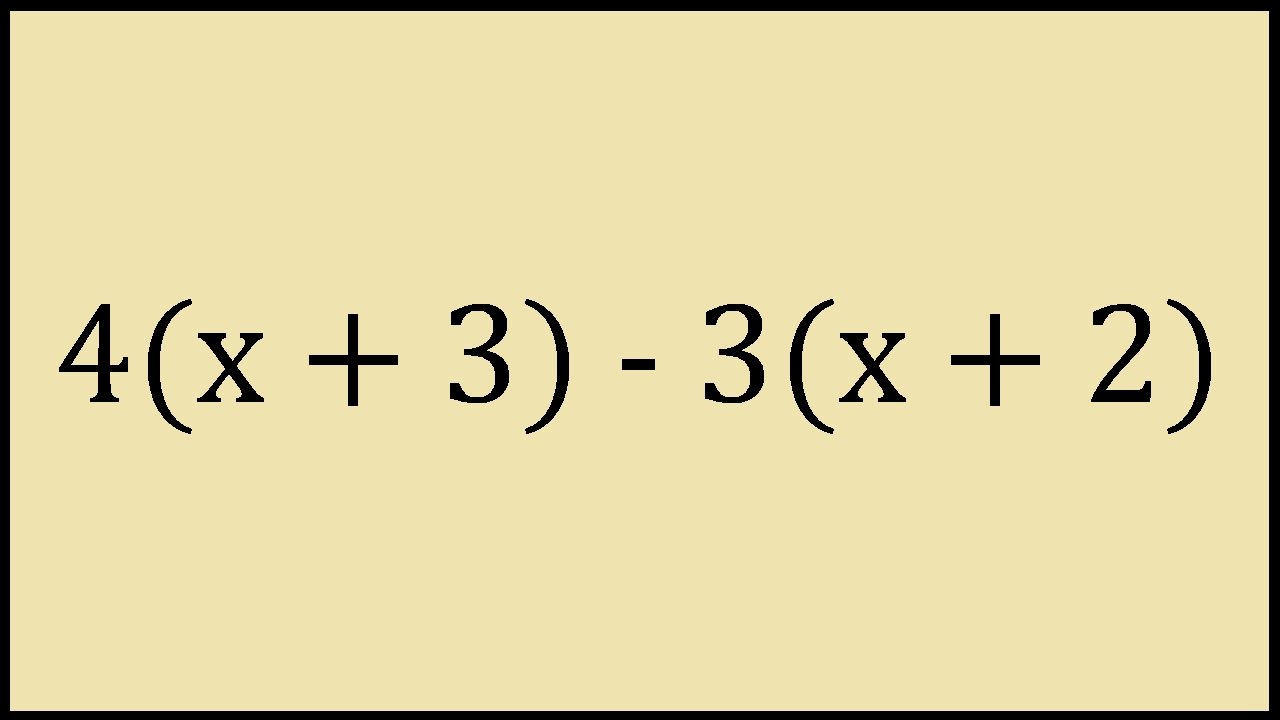
4 X 3 3 X 2 Expand And Simplify Youtube

40 Pin T Type Gpio Adapter Expansion Board For Raspberry Pi 3 2 Model B B A Zero Rpi Part Accessory Toy Parts Accessories Aliexpress

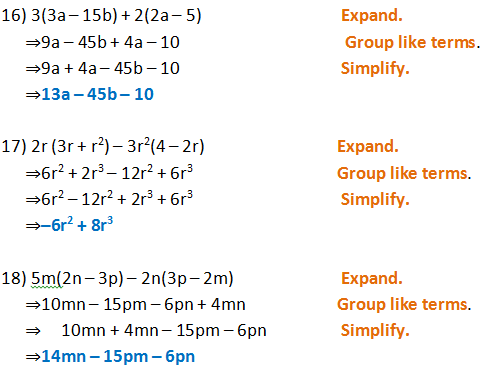
Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths

Misc 9 Expand Using Binomial Theorem 1 X 2 2 X 4 Miscellaneou

Expand And Simplify Trinomial Square A B C 2 A 2 B 2 C 2 2ab 2ac 2bc Youtube

What Is The Expansion Of A B C 3 Quora

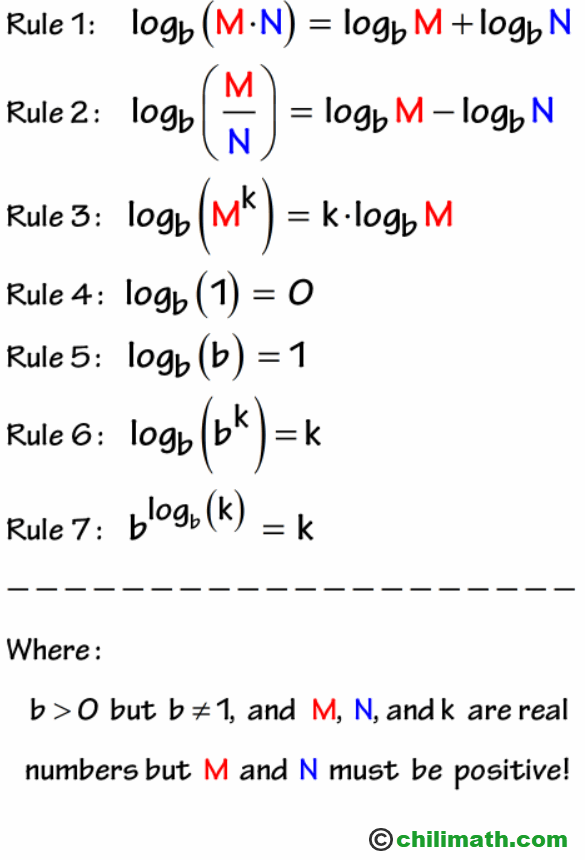
Logarithm Rules Chilimath

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

Amazon Com Haitronic T Type Rpi Gpio Breakout Expansion Board Assembled T Type Gpio Adapter cm Fc40 40pin Flat Ribbon Cable For Raspberry Pi 3 2 Model B B Sc05

Binomial Forms Expansion Of Binomial Expressions Ppt Download

The Middle Term Of The Expansion Of 2x 2 3 3 2x 2 10 Is

A B 4

What Is The Formula Of Math A 3 B 3 Math Quora

Expand And Simplify Binomial Squares 2x 3y 2 Youtube

Q Tbn And9gcq4zpmdaslfjtbs6yv7d6jfr01ay6awvv Z5riovxkoujojjcff Usqp Cau

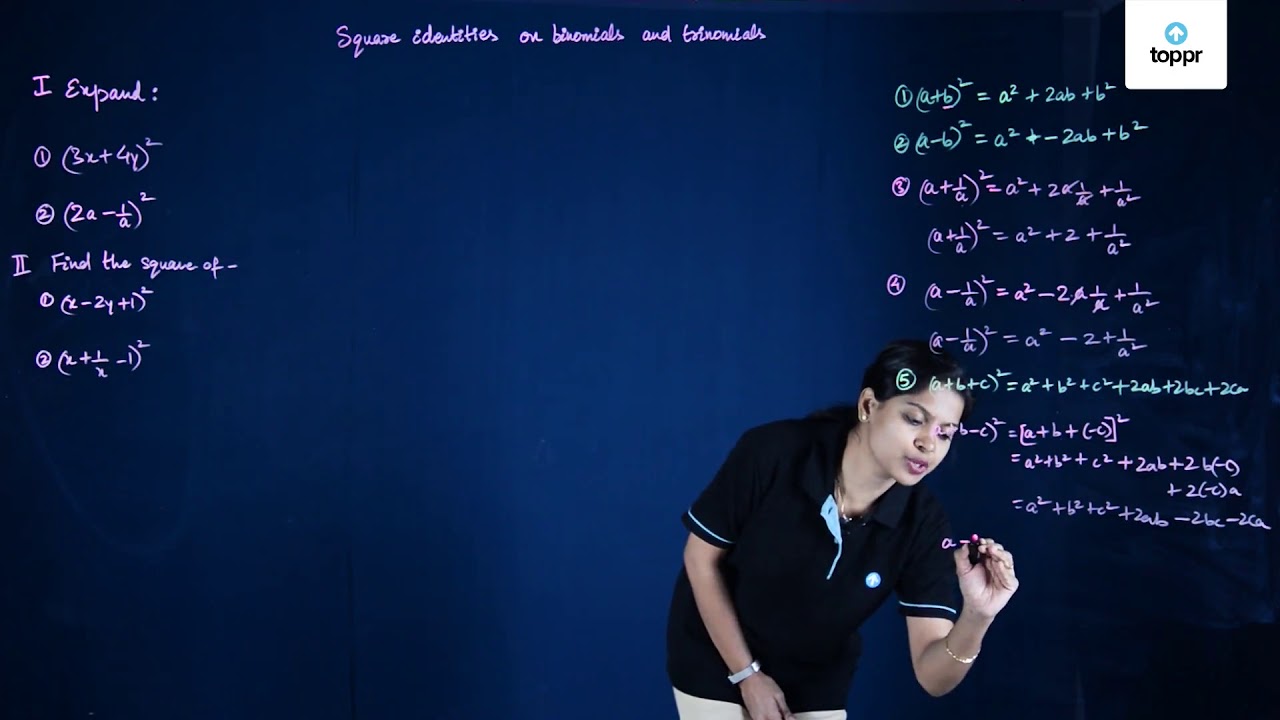
Standard Identities Of Binomials And Trinomials Equations Examples

Misc 1 Find A B N In Expansion Of A B N If First Three

How To Expand Using The Identity A B C 2 B2 C2 2ab 2bc 2ca Youtube

Ex 8 1 3 Expand 2x 3 6 Chapter 8 Class 11 Binomial

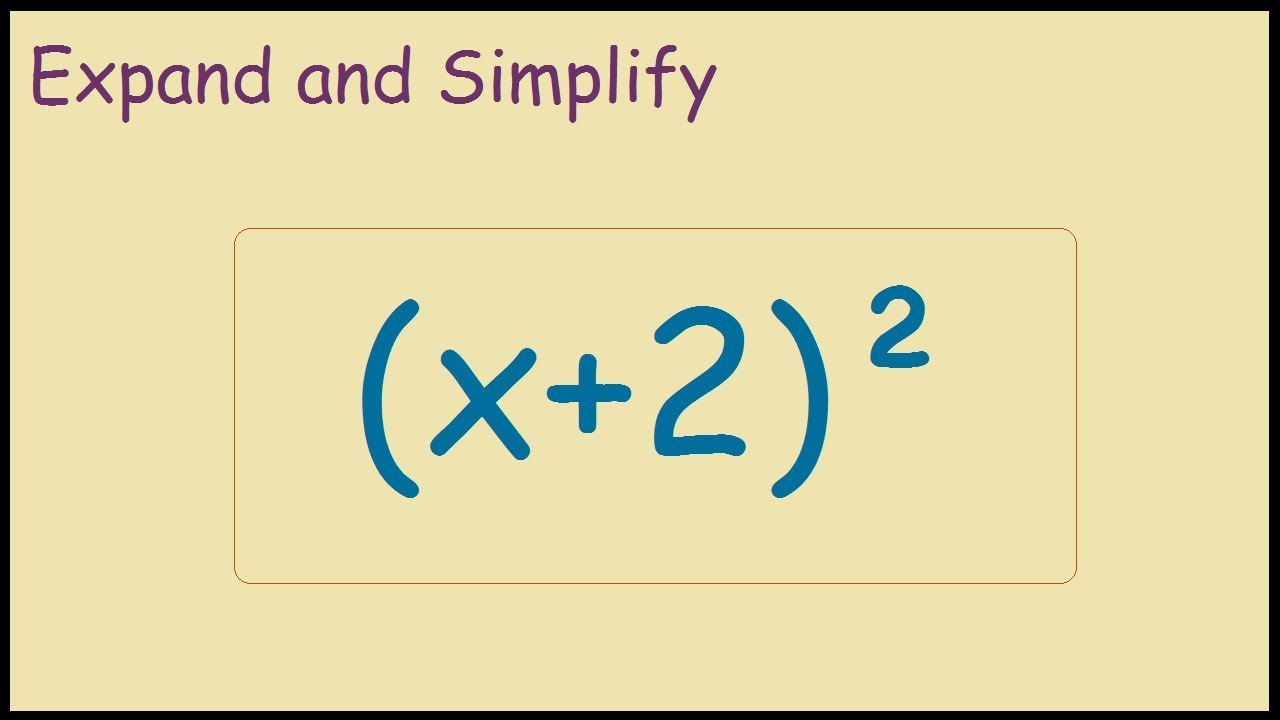
X 2 2 Expand And Simplify Using Foil Method Youtube

Ex 8 1 2 Expand The Expression 2 X X 2 5 Teachoo

Gpio Multi Function Expansion Board For Raspberry Pi B 3 2 Model B Ebay

The Fourth Term In The Expansion Of 1 2x 32 Will Be

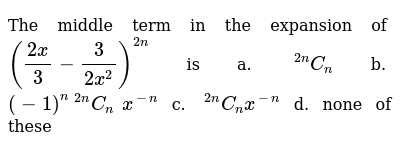
The Middle Term In The Expansion Of 2x 3 3 2x 2 2n Is A

Solved Q1 7 Points Let A 1 2 0 0 3 1 3 2 3 2 1 0 5 0 Chegg Com

Incoming Term: (a+b)^3/2 expansion,